We all are players, playing different roles in different games of our lives. But what do you say? If I call this a simulation like we see in those Sci-fi movies. Everything is automated and we are trying to figure out the rules to make or break the automation processes as we watched in the movie “The Matrix”.
In the 1940s, John Von Neumann was working on self-replicating systems and the core idea was “A robot building another robot”. While working on this project, Neumann gave birth to the “Cellular automaton” a system of building systems, a self-replicator model. Think of this model as RNA molecules in our body that contain all the information to make the exact copy of one’s self. How simple it seems right? but not, building this machine that produces other machines is typically complicated and involves a lot of computing. Despite all the complexities that include producing machines along with their copies, Von Neumann came up with a model in which each square (or a cell) has 29 states that produce the copies of itself.
The concept of this Cellular Automaton became famous when the Mathematician, Martin Gardener published an article in the Mathematical Games column of Scientific American Magazine (Refer to Issue: 1970, October 10th). Conway, a Mathematician who has several noticeable works in Mathematics came up with his amazing work of making the cell unpredictable. Though the inspiration is from Jon Von Neumann’s model, unlike Von Neumann’s 29 states of the cell, Conway’s model has only one square with the two states. The square should be either alive or dead. The dead cells can become alive and vice versa. The rules are very simple, yet the outcomes are completely unpredictable.
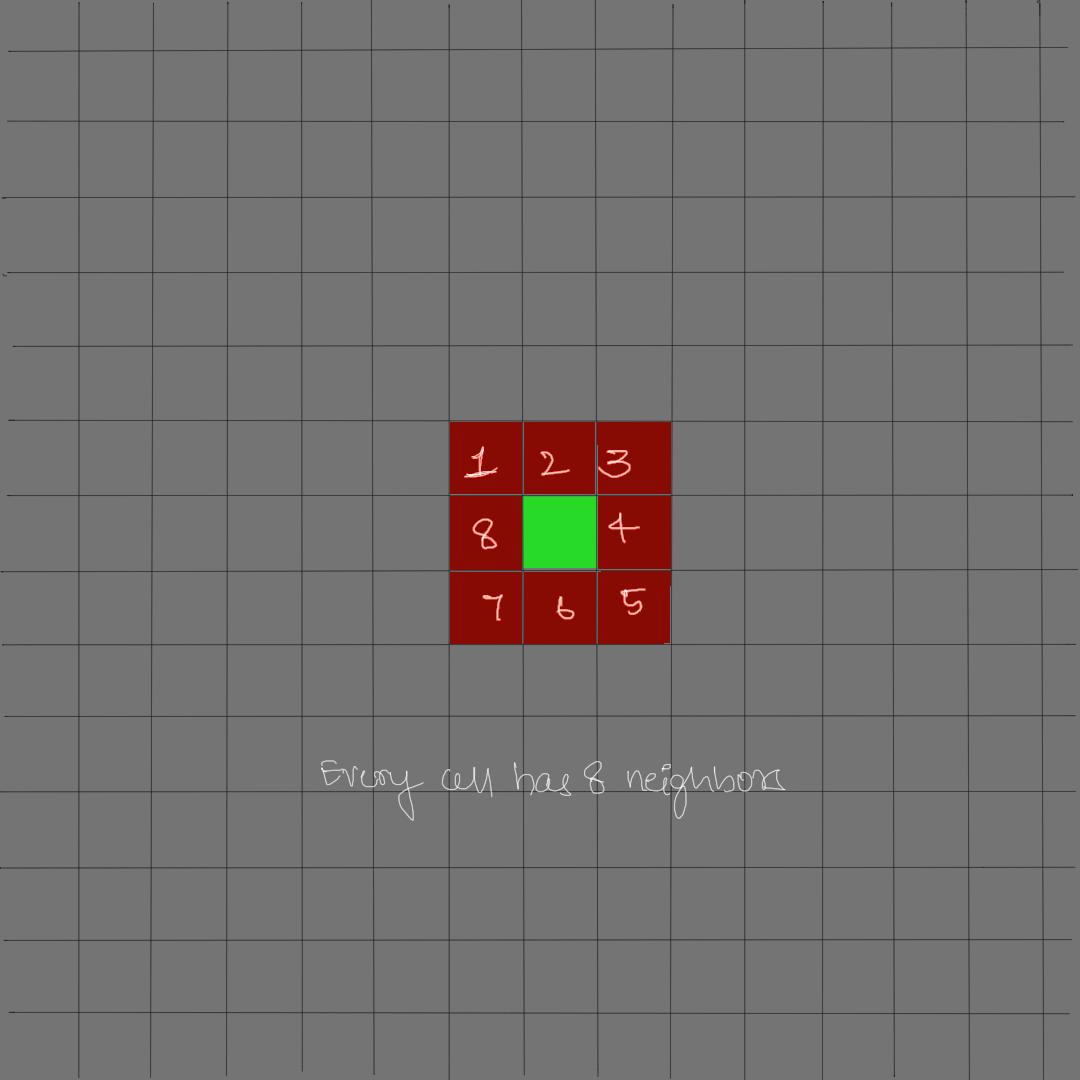
The alive state is highlighted here in the above figure as “Green” and any other cell that is not highlighted is a dead cell. Every cell has 8 neighbours, For instance, observe that green cell in the image. All the red cells are neighbours of the green cell.
The Rules Of The Game.
- Any living cell with less than 2 neighbours will die, because of the underpopulation.
- Any living cell with more than 3 neighbours will die due to overpopulation.
- Any dead cell with exactly 3 living neighbours will come to life and turn into a living cell. You see..! This is the concept of reproduction.
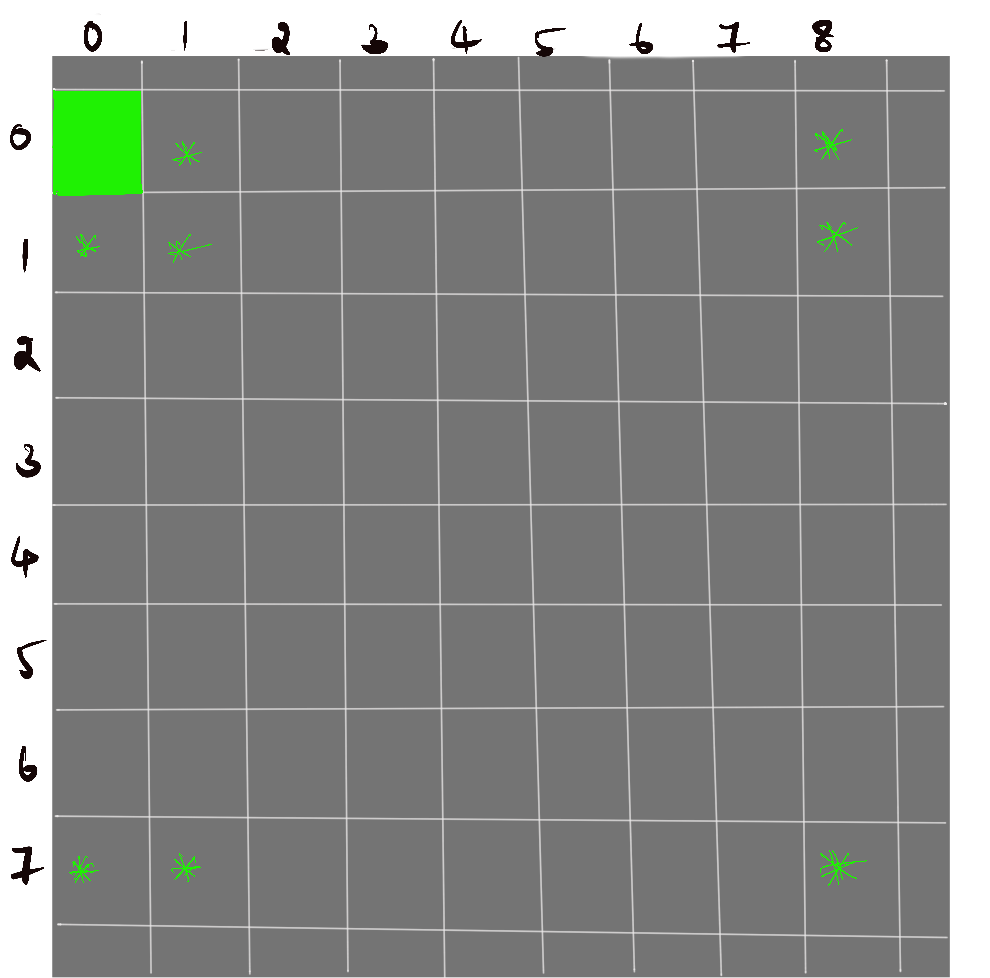
The important thing to note here is the grid follows the Toroidal approach which is nothing but the wrapped grid. That means if you take any edges or corners of the grid, the neighbours lie on all the opposite ends of the grid. For example, consider the grid in the figure below. The neighbours of (0,0) are {(0,1),(1,0),(1,1)}, {(0,7),(7,1)} and the bottom right corner one (7,8). Just like wrapping it to the ends of the grid (Marked as '*')
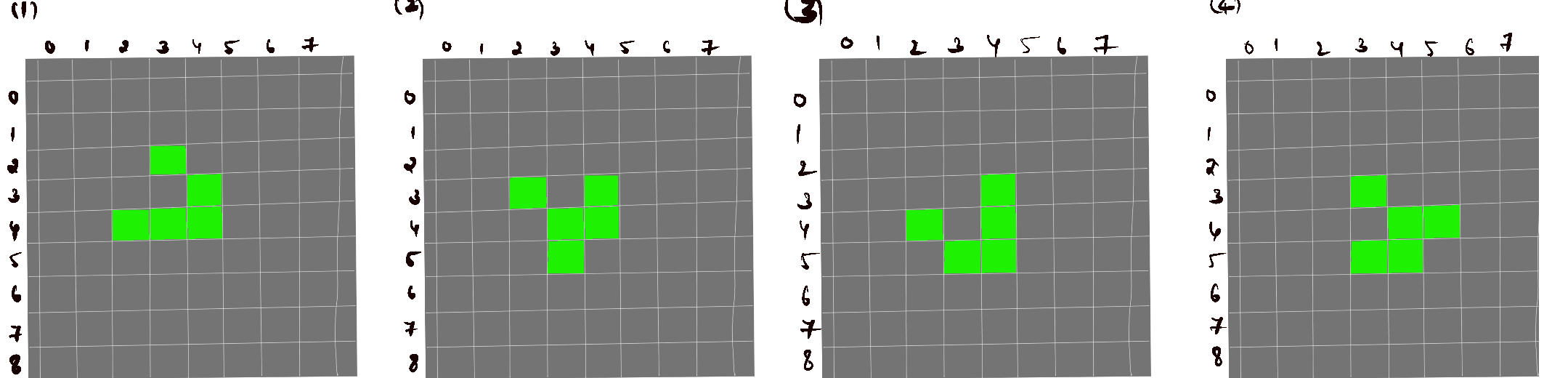
Let us simulate by inputting random cells, observe the four sequential grids (figure 1 to 4) to understand and analyse the process of automaton. At some point all the cells can be dead or the cell can form the symmetry and once the symmetry is reached it can never be gone. Look at these structures for a detailed understanding.
I am no expert in delving deeper into this, but I am always fascinated how nature is built by the maths. If we look deeper in to physics, we can discover the new domain called chemistry and if we look deeper into chemistry we can see something and that is the pure math, just math and this is the secret language of universe. Out of the curiosity and just for sake of fun I tried writing the program to execute this “Conways game” and I entirely credit my teacher Al Sweigart (Though he is not physically teaching me, I am learning through his knowledge ocean available online). I wonder how he simplified the explanation and code for such complex concept. Visit this blog to understand and program it,in python. If you understand the concept of "Lists" in python you are good to go for programming this. The best way to learn math is programming, where you can understand the fundamental blocks like building logics and alanyse the complex parts which you thought that you never would understand so easily.